Историята на тригонометрията: появата и развитието

Историята на тригонометрията е неразривно свързана с астрономията, защото за решаване на проблемите на тази наука древните учени са започнали да изследват връзките на различни количества в триъгълника.

Към днешна дата тригонометрията емикроразделяне на математиката, изучаване на връзката между стойностите на ъглите и дължините на страните на триъгълниците, както и справяне с анализа на алгебричните идентичности на тригонометричните функции.

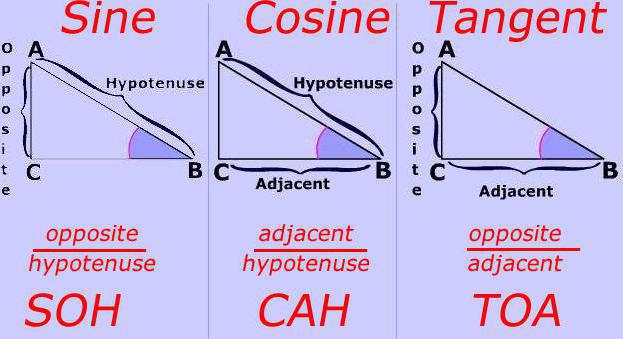
Терминът "тригонометрия"

Самият термин, който даде името на този разделматематика, за първи път е открит в заглавието на книгата, чийто автор е на немския математик Pitiskusa в 1505. Думата "тригонометрия" е от гръцки произход и означава "да се измери триъгълник". За да бъдем по-точни, това не е буквален измерение на тази цифра, но за решението си, че е за определяне на стойностите на своите неизвестни елементи се използват известни.

Обща информация за тригонометрията

Историята на тригонометрията започва повече от двепреди хилядолетия. Първоначално появата му се дължи на необходимостта да се изясни връзката между ъглите и страните на триъгълника. В процеса на изследване е установено, че математическият израз на тези отношения изисква въвеждането на специални тригонометрични функции, първоначално формализирани като числови таблици.

За много математика в съседство с математиката, импулсътразвитието беше само историята на тригонометрията. измервателни Произход ъгъл единици (градуси), свързани с изучаването на древен Вавилон учени, се основава на шестдесетичната система на изчисляване, която е довела до модерното десетичната, се използва в много приложни науки.

Предполага се, че първоначално тригонометриясъществува като част от астрономията. След това се използва в архитектурата. И с течение на времето възниква целесъобразността да се приложи тази наука в различни области на човешката дейност. Това, по-специално, астрономия, море и въздушна навигация, акустика, оптика, електроника, архитектура и др.

Тригонометрия в ранните векове

Водени от данни за останалите научниреликви, изследователите заключават, че историята на възникването на тригонометрията е свързана с работата на гръцкия астроном Хипарх, който за първи път, че за намиране на начини за решаване на триъгълници (сферични). Неговите творби датират от II век пр. Хр.

Това е и един от най-важните постижения на това време е да се определи съотношението на краката и хипотенузата в правоъгълен триъгълник, който по-късно става известен като питагорова теорема.

Историята на развитието на тригонометрията в древна Гърция е свързана с името на астронома Птолемей - автор на геоцентрична система на света, доминиран преди Коперник.

Гръцките астрономи не са знаели за синусите,cosines и допирателни. Те се използват таблици, за да се намери стойността на акорд на кръга с помощта на който може да се сгъва дъга. Устройствата за измерване на акорд бяха градуси, минути и секунди. Един градус е равен на шестдесетата радиус част.

Също така, напреднали проучвания на древните гърциразвитието на сферичната тригонометрия. По-специално, Евклид в "елементи" теорема води по обем закономерности съотношения топки от различни диаметри. Неговите творби в тази област са се превърнали в един вид стимул в развитието на сродни области на знанието. Това е по-специално технологията на астрономическите инструменти, теорията на картографските проекции, системата на небесните координати и т.н.

Средновековие: изследване на индийски учени

Индийските средновековни астрономи постигнаха значителен напредък. Унищожаването на древната наука през IV в. Доведе до движението на центъра за развитие на математиката в Индия.

Историята на тригонометрията катоотделен раздел на математическото обучение започва през Средновековието. Тогава учените заменят акордите със синусите. Това откритие ни позволи да въведем функции, свързани с изучаването на страните и ъглите на триъгълник с прави ъгъл. Тоест, то тогава тригонометрията започна да се отделя от астрономията, превръщайки се в клон на математиката.

Първите таблици на санитарите бяха в Ариабхата, те бяха проведени през 3^за, 4^за, 5^за, По-късно се появиха подробни версии на масите: по-конкретно, Бхаскара изброи задължителната таблица след 1^за.

Първият специализиран трактат натригонометрия появи в X-XI век. Неин автор е на Централна Азия учен Ал-Бируни. И в основната си работа "The Canon Масуд" (Книга III) средновековен автор дори по-дълбоко в тригонометрията, което води до задължително маса (на стъпки от 15 "), както и таблица на допирателни (на стъпки от 1 °).

История на развитието на тригонометрията в Европа

След превеждането на арабските трактати на латински(XII-XIII в), повечето от идеите на индийските и персийските учени бяха заимствани от европейската наука. Първите споменавания на тригонометрията в Европа датират от XII век.

Според изследователите, историята на тригонометрията вЕвропа е свързана с името на англичанина Ричард от Уолингфорд, който стана автор на произведението "Четири предания върху преки и обърнати акорди". Това е неговата работа, която стана първото произведение, което е изцяло посветено на тригонометрията. До петнадесети век много автори в своите писания споменават тригонометрични функции.

Историята на тригонометрията: Новото време

В днешно време повечето учени започнаха да осъзнаватизключителната важност на тригонометрията не само в астрономията и астрологията, но и в други области на живота. Това е преди всичко артилерия, оптика и навигация в дългосрочни кампании. Поради това през втората половина на 16 век тази тема се интересува от много изтъкнати хора от онова време, включително Никола Коперник, Йоханес Кеплер, Франсоа Виета. Коперник придава тригонометрия на няколко глави от неговия трактат "За въртенето на небесните сфери" (1543). Малко по-късно, през 60-те години на XVI век, Ретик - ученик на Коперник - води в своята работа "Оптична част на астрономията" петнадесетцифрени тригонометрични таблици.

Франсоа Виет в "Математическия канон" (1579 г.)дава подробно и систематично, макар и непроверено описание на плоската и сферична тригонометрия. А Албрехт Дюрер стана онзи, благодарение на когото се появи синусоида.

Заслугите на Леонард Ойлер

Задействането на съвременното съдържание иГледката беше направена от Леонард Ойлер. Неговият трактат "Въведение в анализа на безкрайността" (1748) съдържа определението на понятието "тригонометрични функции", което е еквивалентно на модерното. По този начин този учен е успял да определи обратните функции. Но това не е всичко.

Определението на тригонометричните функции като цялоцифровата права линия стана възможна благодарение на изследването на Ойлер не само за допустими отрицателни ъгли, но и за ъгли с повече от 360 °. В неговите творби той доказа, че за пръв път косинусът и тангентът на правилния ъгъл са отрицателни. Разграждането на цели степени на косинус и синус също стана заслуга на този учен. Общата теория на тригонометричните серии и изследването на конвергенцията на получените серии не бяха обекти на изследванията на Ойлер. Въпреки това, работейки по решаване на подобни проблеми, той направи много открития в тази област. Благодарение на работата му продължи историята на тригонометрията. В творбите си той накратко докосна въпросите на сферичната тригонометрия.

Области на приложение на тригонометрия

Тригонометрията не се отнася за приложните науки, вИстинският ежедневен живот на задачата рядко се използва. Този факт обаче не намалява неговата значимост. Много важно, например, е техниката на триангулация, която позволява на астрономите да измерват точно разстоянието до близките звезди и да контролират сателитните навигационни системи.

Също така тригонометрията се използва в навигацията, теориямузика, акустика, оптика, анализ на финансовите пазари, електроника, теория на вероятностите, статистика, биология, медицина (например, в дешифриране ултразвук ултразвук и компютърна томография), фармация, химия, теория на числата, сеизмология, метеорология, океанография, картография, много раздели физиката, топография и геодезия, архитектура, фонетиката, икономика, електронна техника, машиностроенето, компютърна графика, кристалография, и така нататък. д. историята на тригонометрията и нейната роля в изследването на природни и математически науки се изучават и до днес. Може би в бъдеще, нейните приложения ще бъдат още по-големи.

История на произхода на основните понятия

Историята на произхода и развитието на тригонометрията има повече от един век. Въвеждането на понятията, които са в основата на този раздел от математическата наука, също не е моментно.

Така че понятието "задължително" има много дълга история. Споменаването на различните отношения на сегменти от триъгълници и кръгове се открива дори в научни трудове, датиращи от III век пр.н.е. Творбите на такива велики древни учени като Евклид, Архимед, Аполоний Пергски вече съдържат първите изследвания на тези отношения. Новите открития изискват определени терминологични усъвършенствания. По този начин индийският учен Aryabhata дава на акорд името "jiva", което означава "низ". Когато арабските математически текстове бяха преведени на латински, терминът беше заменен със задължително със същата стойност (т.е. "огъване").

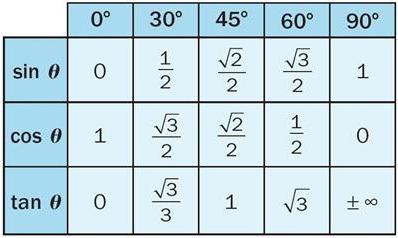
Думата "косинус" се появи много по-късно. Този термин е съкратена версия на латинската фраза "допълнителен задължителен".

Произходът на тангентите е свързан с декодиранепроблеми с определянето на дължината на сянката. Терминът "допирателна" е въведен през 10-ти век от арабския математик Abul-Wafa, който е съставил първите маси за определяне на тангентите и котангентите. Но европейските учени не са знаели за тези постижения. Германският математик и астроном Ремомантън преоткрива тези понятия през 1467 г. Доказателството за теоремата на допирателните е неговата заслуга. И терминът се превежда като "отнасящ се".